In 2004 my son introduced me to a new board game.  Quoridor came from Gigamic Games, a French company.^[1]   The game had been around since the 1990’s but I had not seen it before.  Up to four people can play; however, I have only ever played with one opponent.  My son beat me most of the time—he had played a few games before showing the game to me.

    Around the same time, a colleague was raving about the Ruby programming language^[2] and I became curious to understand his enthusiasm.

    Quoridor is a maze game.  On searching Google (in 2004) to see if anyone had devised a notation for recording games, I found little of interest—except the rules of play, which I already knew.  The game uses a 9 x 9 cell board, one more row and column than chess or checkers.  Each player has one piece called a pawn, which resembles a chess pawn.

    At the start of play each player’s pawn is placed on the cell (or square) of the middle file and the rank closest to the player.  The object is to be the first to advance one’s pawn to the opponent’s starting rank (called the goal rank), moving one square at a time, except when “jumping” the opponent’s pawn.  However, there is more to the game than pushing pawns!


    Each player also has an allocation of ten fences.  The player on turn can either move his pawn or place a fence on the board.  Fences are used to construct a maze and all have the same color because there is just one maze.  As the name implies, fences block pawns.  The idea when placing a fence is to make it harder for the opponent to reach his or her goal, or easier for the player.   Therefore, maze construction strategies are crucial to success in the game.

    At the same time, Quoridor rules prohibit completely blocking a player’s access to the goal.  Therefore the maze, to which both players contribute fences, must remain solvable for both players.


    In chess, the algebraic system for recording moves uses letters for files and numbers for ranks.  Files are labeled a – h, from white’s left to right, and again from white’s side, ranks are numbered 1 – 8.  It seemed logical to label Quoridor cells similarly, using just one extra letter and number.

    Pawn moves in chess are often recorded using a shortcut that identifies the target square only.  Thus, the move e2-e4 in chess can be abbreviated e4.  When applied to Quoridor this convention reduces the notation for pawn moves to the abbreviated two-character form.  For example, at the start of a game the white pawn occupies square e1 (middle file, white’s back rank).  In shortcut form the move from e1 to e2 can be recorded simply as e2.

    Fence placements are a little trickier to notate.  Once placed, a fence does not move.  However, the placement can be either horizontal (parallel to a rank) or vertical (parallel to a file).  Each fence blocks two adjacent cells, belonging to the same rank or the same file.

    Since fences are two squares in length and are placed between cells there are only 8 horizontal fence slots between each pair of adjacent ranks and 8 vertical fence slots between each pair of adjacent files on the Quoridor board.  With these facts in mind, an efficient way to record fence placements would be to use one number and two letters for a horizontal fence, or one letter followed by two numbers for a vertical fence.

    Thus a horizontal fence placed between squares e1, f1 and e2, f2 was recorded as move 1ef.  A vertical fence between squares f2, f3 and g2, g3 was recorded as f23.  In other words, a horizontal fence was identified by the letter of the rank below it, while a vertical fence placement used the number of the file to its left.  This convention is consistent with labeling fence slots with the letters a to h (left to right from white’s home side), and the numbers 1 to 8 (from bottom to top).

    At the time of devising this notation I was not aware of any existing notation scheme for Quoridor.  Here is how the first few moves of a game might appear when recorded with this system.



    I began to program Quoridor in Ruby before acquiring a sound understanding of either Quoridor or Ruby.  Strictly speaking I began to program the engine part of Quoridor—the part that plays the game, setting aside the human interface for later.  To exercise the evolving program I would either insert data directly into the code, or have the program read moves from a text file.

    One of the realities of computer programming is that somebody else always does it better, or nearly always, provided the project is interesting.  In 2004, the Internet had little or nothing to say about Quoridor and I did not find a single program to play the game.  However, at the time of this writing ten years later, the term Quoridor returns more than 200,000 Google hits.  If 199,000 of them were irrelevant, the results would still include many interesting pages.

    Recently I downloaded a Java program that plays Quoridor.^[3]  I did not immediately play a game, fearing that to do so might discourage me from writing my own Quoridor story, but after awhile I played a few games against the program, winning all of them easily.  I thought that if my program were matched against the Java program, mine would win. However, that conclusion was wrong, as will be illustrated later on this page.

    The Java program that I downloaded has a very nice user interface.  Pawns are colored circles, and fences broad black lines.  Later I will describe the different kind of user interface that I made for Ruby Quoridor.


    At the time of starting this project I knew nothing about maze solving. However, while Google did not have much to say about Quoridor in 2004, it did return useful results about maze algorithms.  After probably insufficient study, I settled on the Bellman Flood method.   But first I should summarize how game states were represented in Ruby. To fully describe a Quoridor position one needs to know the following:


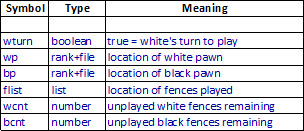
    Everything in Ruby is an object, including numbers.  The ‘Type’ column in the above table is intended as descriptive, not necessarily to name a Ruby data type or class. The Game object consisted of a list of moves (pawn moves or fence placements).  Thus the current state at any point in the game, after any number of moves have been played, may be described using the six terms summarized in the table.

    The first Ruby-specific construct that I explored was the hash class.   The program constructed an index using a hash named fxref.  Hash keys were the coordinates of a cell (or square) and the index named squares that had an adjacent fence.  To traverse the fence index the program used the fxref.each method, while fxref.has_key?(square) returned whether or not the index contained the identified square. Looking back I wonder why I didn’t make hashes for the squares on both sides of a fence, and separate hashes for vertical and horizontal fences.

    Once the mechanics of the game were functioning properly, such things as not allowing fences to be placed on top of existing fences or to pass through them, making sure that the maze remained solvable, not allowing pawns to pass through fences, not allowing pawn moves to an occupied square, allowing jumps when one jump path is blocked but another is open, etc.—after all this it was time to think about move evaluation.

    A reasonable starting point for the evaluation would be to generate a random move.  Make each pawn move equally likely and each legal fence placement equally likely.  Then do one or the other in some pre-determined proportion.   Of course, this is sure to produce a very bad game, but the point is to make the program play a legal game.

    Although my own playing experience was very limited, I devised a few concepts and rules to assist in defining the program’s position evaluation and consequent move generation.  The thought was that by playing games against the program and experimenting with parameter values, it should be possible to improve the program’s play.


    Bellman number – the minimum number of pawn moves required to reach the goal from the current position.

    Score – Program’s Bellman number minus opponent’s Bellman number (smaller is better).

    Resigns – Program has no fence moves (all of program’s fences have been placed) and the best possible pawn move leads to certain loss. The Ruby program does not continue playing when defeat is assured.


    Pan-pan – The opponent’s pawn is advanced on an unblocked edge file before the game itself has reached an approximate midpoint (urgent attention required).

    Mayday – The opponent threatens to win on the next move (emergency action required).


    Evaluation parameter – Constant to be added or subtracted from the evaluation, based on characteristics of the position.  For example –



    Generate pawn move – Generate all possible pawn moves.  Prune list to those with equal best evaluations.  Randomly select one of the latter.

    Generate fence placement – Generate all possible fence placements.  Prune list to those with equal best evaluations.  Randomly select one of the latter.

    Generate move – Choose between best pawn move and best fence move, based upon multiple evaluation factors including: urgency, score improvement, game stage (number of moves completed and number of fences placed), positional factors (how restricted are paths), and so forth.

    When generating a move, the program, of course, verifies that the move to be played does not render the maze unsolvable for either player.  (Only legal fence placements are generated.)


    My son (who introduced me to the Quoridor game) was interested in the technical as well as the artistic aspects of photography.  This gave me the idea to create a user interface, based on photographs of the board and playing pieces.

    To get started on this we set up a jig to position my old Kodak digital camera over a table, and aimed straight down.  On the table surface we placed a white poster board and, on top of that, the Quoridor board.  My son and I shot many photos.  We put one pawn on a central square of the board and took repeated photos with different colored pawns.  Similarly we took shots with one fence, two fences, three fences, etc. on the fence rows.  Then we photographed one horizontal fence on a board fence slot, and one vertical fence.

    On examining the photos, the first problem was that the camera lens distorted the board shape (left).  It was not square, not even close.  Upon further reflection that did not seem important, because I had in mind constructing the board image, using one individual square photo.  Similarly, the fence row would be constructed from uniform fence squares.

    After reviewing the raw photos I realized that to superimpose a pawn image on top of a square, and to make it slide from one square to another, would require having transparent pawn images.  I used Photoshop® (the light edition) to create suitable transparent images from photos.


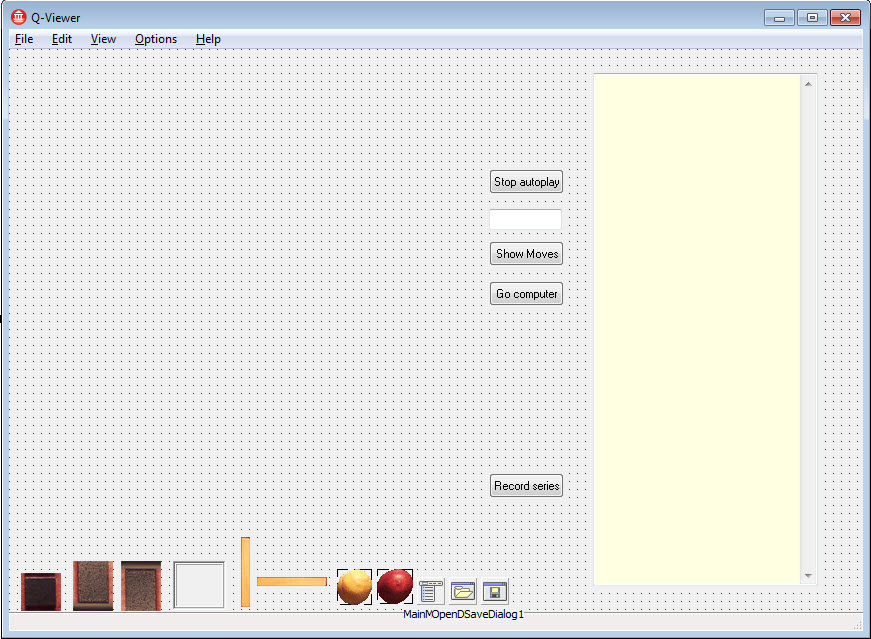
    I no longer have an active Delphi 7 development environment.  The design-time image of the “Q-Viewer” user interface (above) was recreated in the Embarcadero XE2 IDE.  The program’s (Pascal) code that generates the main form constructs a playing board, made up of individual inside- and edge-squares, and so forth.


    The illustration above shows the starting position for a game, in the (running) Q-Viewer interface.  The board is a little too perfect.  That is because all the squares are the same.  The lighting is uniform throughout and all the fences are identical.  There is no variation in the wood grain!

    Earlier I mentioned that I had downloaded a Java implementation of Quoridor by Martijn van Steenbergen, and had played a few games with it.  Then, although it was exceedingly awkward to do so, I pitted the Java program against the Ruby program for one game.  It was necessary to input the moves for both programs manually, and with great care!

    Before starting this game I thought that my Ruby program would win, but it did not.  It lost quite disgracefully.

    The illustration below shows a key position in the game. The yellow panel displays moves that have been played up to the present move.  In the illustration I had not yet entered the Ruby program’s current move e56 on the Java board.


    At the point shown, black has placed all ten fences.  Hence the game may be considered in the end stage.  The number of pawn moves required for white to reach the goal rank is 18.  Black on the other hand, has two routes to the goal, the shorter being by way of a5-a4.  That is in fact the route that black selected, making the game an easy theoretical win for white.

    When black reached a4, white responded promisingly by placing a horizontal fence to block the a-file.  Black continued b4.  By this time, the Ruby program should have been rejoicing, as it only needed to continue the charade until black reached, say d4, and then place a vertical fence at d34, forcing black to backtrack all the way to g7.  Instead the program reached deep into its stupid mode, allowing black to pass d4 unmolested, and then turn south, with only minor annoyances along the way.  In short, the Ruby program lost this game!

    My memory for long-completed (or abandoned) projects is poor. When something unexpected happens, such as the play described in the preceding paragraph, I want to revisit the program, uncover what caused the bad move choice, and fix it. But it is unlikely that I will do that, because the Quoridor / Ruby project was of the past, while the present and future hold more inviting projects than there are hours in the day.

---

^[1] http://en.gigamic.com
^[2] https://www.ruby-lang.org/en/
^[3] http://martijn.van.steenbergen.nl/projects/quoridor/